Karl Entacher

Über die Wärmeleitungsgleichung

K. Entacher
Fachhochschule Salzburg, Urstein Süd 1, 5412 Puch

Von 1804 bis 1807 entstand die wohl wichtigste und preisgekrönte Arbeit von Baron Joseph Fourier, publiziert 1822:

Theorie analytique de la chaleur
(The Analytical Theory of Heat)
Jean Baptiste Joseph Fourier (1768 bis 1830).

Fourier hat die Wärmeentwicklung in einem homogenen Körper durch eine Differentialgleichung (Wärmeleitungsgleichung) beschrieben und diese Gleichung mittels der nach ihm benannten Methode der trigonometrischen Reihen gelöst.

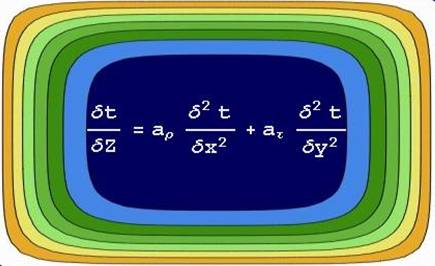
Unter der Wärmeleitungsgleichung versteht man im Allgemeinen eine partielle Differentialgleichung, welche die Temperaturentwicklung im Zeitpunkt t an einer beliebigen inneren Stelle (x,y,z) eines dreidimensionalen Objekts beschreibt. Diese Gleichung hat die Form:

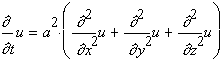
Die Lösung der Differentialgleichung, d.h. die Funktion u(t,x,y,z), beschreibt die Temperaturentwicklung im Zeitpunkt t an einer beliebigen inneren Stelle (x,y,z) eines dreidimensionalen Objekts. Die "Materialkonstante" a definiert hierbei die Temperaturleitfähigkeit (Diffusität) für ein homogenes isotropes Material.

Um 1930 adaptierte J.D. MacLean [MLe30,MLe32] Fourier‘s Differentialgleichung um die Wärmeleitung in Holz zu beschreiben. Da es sich bei Holz um keinen homogenen Körper handelt, musste MacLean die Wärmeausbreitung in tangential- und radialer Richtung unterschiedlich berücksichtigen. Unter Zugrundelegung eines unendlich langen Balkens (dies ist aufgrund der vielfachen Längenausdehnung eines Holzbalkens bezogen auf die restlichen Balkenabmessungen möglich) und des anisotropen Temperaturleitungsverhaltens von Holz kann diese Gleichung folgendermaßen angepasst werden

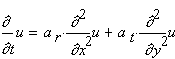
Die Variable z wird vernachlässigt, d.h. man reduziert auf eine Temperaturfunktion u(t,x,y). Die Faktoren ar und at entsprechen der Temperaturfähigkeit in radialer und tangentialer Richtung des Holzes und ihre Berechnung ist in [Kol51,Vor58] dargestellt. Die Arbeit von MacLean ist Grundlage für viele wärmetechnische Problemstellungen in der Holztechnologie wie Holztrocknung, Termoholz, Dämmverhalten von Holz (Wänden), uvm.

Im Folgenden wird die Temperaturverteilung in einem quadratischen Holzbalken grafisch dargestellt. Dazu wird der Balkenquerschnitt diskretisiert und die Temperatur an jedem diskreten Punkt des Querschnitts mittels der Lösung der MacLean Gleichung berechnet und in einer Datenmatrix gespeichert. Ein Flächendiagramm visualisiert diese Matrix und damit die Temperaturverteilung im Balken. Die Verteilung wird in folgenden Grafiken für die Zeiten t = 10 und t = 30 Minuten visualisiert. Es wurde eine Balkenanfangstemperatur von 21 Grad vorausgesetzt und eine Erwärmung des Balkens mit 100 Grad.

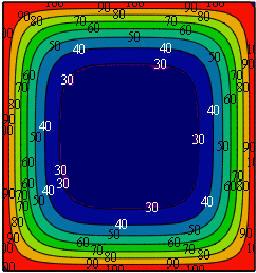
Durch Berechnung der Temperaturverteilung für verschiedene Zeitpunkte und geeigneter Anordnung der Grafiken erhält man folgende Illustration (Weitere Bilder):

Literatur

[MLe30] MacLean, J.D. Studies of heat conduction in wood, Proceedings of the Twenty-Eight Annual Meeting of the American Wood Preservers Association, Seattle, 1930.

[MLe32] MacLean, J.D. Studies of heat conduction in wood, Part II, Proceedings of the Twenty-Eight Annual Meeting of the American Wood Preservers Association, St. Louis, 1930.

[Kol51] Kollmann, F. Technologie des Holzes und der Holzwerkstoffe, Band 1-3, zweite Auflage, Springer Verlag, 1951.

[Vor58] Vorreiter, L. Holztechnologisches Handbuch Band II.Verlag Georg Fromme & Co. Wien, 1958.

Matlab Code

function tsum = tempsum(x,y,z)
t0 = 20; t1 = 120;
p=pi^2;
b = 10;h = 10;
ar = 0.035; at = 0.035;
s = 0;
for n = 1:10
    for m = 1:10
        tmp = 0;
        nn = 2*n-1; mm = 2*m-1;
        tmp = (exp((-p)*z*(((ar*mm^2)/b^2) +
        ((at*nn^2)/h^2)))*sin(mm*pi*x/b)*sin(nn*pi*y/h))/(mm*nn);
        s = s + tmp;
    end
end
tsum = t1 + ((t0-t1)*16/p)*s;

for i = 1:N+1
    for j = 1:N+1
        M(i,j) = tempsum((i-1)*b/N, (j-1)*h/N, 50);
    end
end
contourf(M);
axis equal;
axis off;